Hostouň je startovacím (i cílovým) místem naší nedělní dopolední procházky. Pokračujeme tak v našich „zimních“ půldenních procházkách.
Hlavním motivem proč Hostouň je vyřešení matematicko-fyzikální geocachingové serie – pro vyřešení byla potřeba znalost (případně nalezení) příslušných hodnot.
Luštení bylo zajímavé, samotné umístění kešek v (Hostouň a okolí) už tolik ne.
Zkusíš také odpovědět? Zadání jsou převzata z listingu jednotlivých kešek.
Kontrolu správnosti odpovědí si můžeš ověřit na našem emailu.
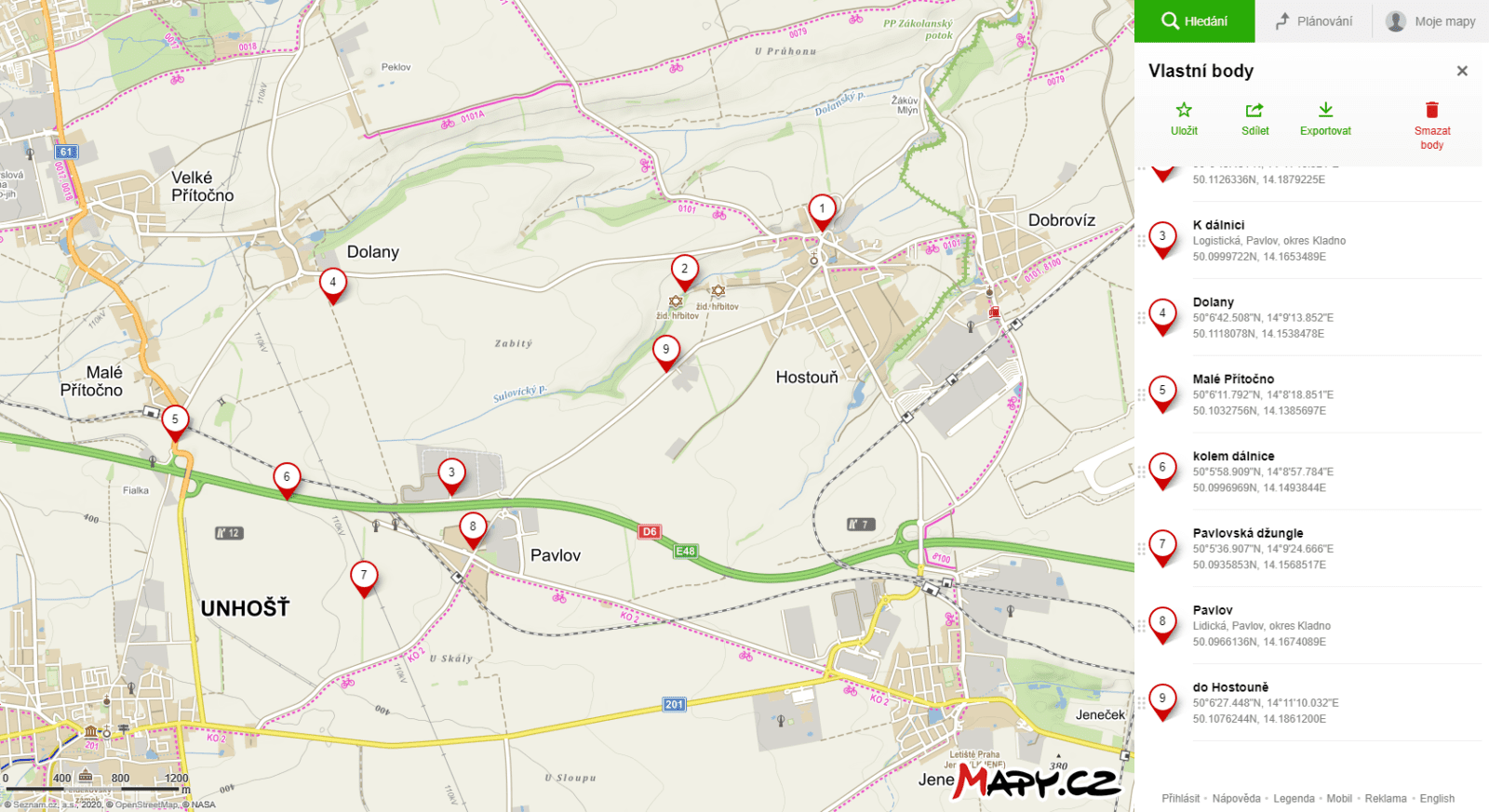
Plánek Hostouň
Hostouňská náves
Parkujeme na návsi (Hostouň). V obci odlovíme jednu místní kešku a pak už vyrážíme na trať. Náš týmový logistik připravil – jako obvykle – optimální trasu tak, abychom po okruhu zvládli i několik dalších zajímavých míst / kešek.


Erdősovo číslo
Erdősovo číslo je pseudomatematický pojem zavedený na počest proslulého maďarského matematika Pála Erdőse (1913-1996). Ten byl známý tím, že neustále cestoval mezi nejrůznějšími matematickými konferencemi a institucemi po celém světě, díky čemuž na světě žilo (a mnohdy ještě žije) několik set matematiků, kteří jsou podepsáni jako spoluautoři pod některým jeho odborným článkem. Erdős za svůj život publikoval více článků, než kterýkoliv jiný matematik (minimálně 1525).
Erdősovo číslo vzniklo jako humorná klasifikace matematiků podle toho, jak moc jsou autorsky vzdáleni od Pála Erdőse. Aby člověk získal své Erdősovo číslo, musí být napsán jako spoluautor odborného článku s osobou, která už číslo má. Definice čísla vypadá takto: Pál Erdős má číslo 0. Všichni, kdo s ním jsou podepsáni pod odborným článkem, mají číslo 1. Lidé, kteří někdy spolupracovali s nimi, ale ne přímo s Erdősem, mají číslo 2 atd.


Faradayova konstanta
Faradayova konstanta vyjadřuje poměr mezi molární hmotností a elektrochemickým ekvivalentem látky. Také je to celkový elektrický náboj 1 molu látky úplně disociované nebo ionizované na částice s elementárním nábojem. Faradayova konstanta se používá při výpočtech pomocí Faradayových zákonů elektrolýzy. Její značka je F a je tvořena součinem elementárního náboje a Avogadrovy konstanty.
A: Počet číslic před desetinnou čárkou.
B: Jaká číslice za desetinnou čárkou je nejvyšší?
C: Jaká číslice za desetinnou čárkou je druhá nejvyšší?
D: Jaká číslice za desetinnou čárkou se opakuje nejvíce krát?



Permeabilita vakua
μ0
Permeabilita je v fyzikální veličina, která vyjadřuje vliv určitého materiálu nebo prostředí na výsledné účinky působícího magnetického pole. Některá prostředí tyto účinky zesilují, jiná je zeslabují a existují také prostředí bez tohoto vlivu.
Permeabilita vakua je koeficientem úměrnosti mezi veličinami B a H ve vakuu, kde B je magnetická indukce a H intenzita magnetického pole. Obě tyto veličiny charakterizují magnetické pole; to může být ve vakuu vytvářeno pohybujícím se elektrickým nábojem, tedy rovněž elektrickým proudem, změnou elektrického pole v čase nebo obojím, tudíž obě tyto veličiny jsou úměrné těmto vytvářejícím vlivům.
Rozdíl
Jejich rozdíl pak spočívá jednak v tom, že B zohledňuje vliv látky v prostředí, jímž se pole šíří, a dále v tom, že magnetická indukce je definována prostřednictvím síly, kterou pole působí na pohybující se náboj, zatímco intenzita magnetického pole nikoliv. Ve vakuu je vliv látky odstraněn a permabilita vakua je tedy koeficient doplňující výrazy s faktory vytvářejícími magnetické pole tak, aby ve vakuu odpovídaly silovému působení pole – buď přímo, ve vztazích pro sílu, nebo nepřímo, prostřednictvím magnetické indukce.
A: Jedno z vyjádření konstanty obsahuje i násobek Pí, kolika násobek?
B: Jaká číslice je jako exponent ve vyjádření obsahující zmíněné Pí?
C: Jaká číslice je jako exponent v základním vyjádření konstanty?
D: Jaká číslice je před desetinnou čárkou v základním vyjádření konstanty?



Permitivita vakua
ε0
Permitivita vakua je fyzikální konstanta. Hodnota permitivity vakua je fixována stávající definicí ampéru, jedná se tedy o dohodnutou konstantu, nikoli o měřenou veličinu. Podle připravovaných nových definic SI by se již jednalo o veličinu zatíženou experimentální chybou (neboť permeabilita vakua již nebude definována přesně). Permitivita vakua se vyskytuje např. v Coulombově zákoně pro elektrickou sílu mezi dvěma elektricky nabitými tělesy ve vakuu. Velikost permitivity vakua nezávisí na směru ani rychlosti pohybu pozorovatele, což souvisí s teorií relativity. (zdroj: wiki)
AB: Ciferný součet prvních šesti nenulových cifer konstanty.
C: Rozdíl mezi první a druhou nenulovou číslicí konstanty.
D: Jaká je největší cifra konstanty?
E: Jaká je nejmenší nenulová cifra konstanty?


Zlatý řez
φ
Zlatý řez vznikne rozdělením úsečky na dvě části tak, že poměr větší části k menší je stejný jako poměr celé úsečky k větší části. Je to iracionální číslo. Již nejméně od renesance využívají zlatý řez umělci ve svých dílech, zejména ve formě tzv. zlatého obdélníku, ve kterém se zlatý řez vyskytuje jako poměr stran. Působí prý totiž esteticky příznivým dojmem. Obdélník, jehož poměr stran odpovídá zlatému řezu, lze rozdělit na čtverec a obdélník, jehož poměr stran opět odpovídá zlatému řezu.
Fibonacci
Zlatý řez se vyskytuje v přírodě ve formě Fibonacciho posloupnosti. Listy rostlin, pokud vyrůstají jednotlivě, jsou na větvičkách rozloženy tak, že každý list vyrůstá nad předchozím listem více či méně posunut o určitý úhel. V dolní části stonku jsou listy starší a větší, u vrcholu mladší a menší. Všechny listy jsou stejnoměrně osvětlovány Sluncem, menší nestíní větším, které mají delší řapíky. Dalším projevem zlatého řezu je uspořádání semen slunečnice nebo smrková šiška, ve které jsou šupiny rozmístěny jako spirála, nebo točité schody.
Ananas
Toto rozmístění je také velice dobře vidět u ananasu. Dalším projevem zlatého řezu v přírodě je logaritmická spirála, která nemění tvar a roste stejně do délky i do šířky. Jejím projevem je růst neživých částí živého tvora. Mohou to být vlasy, nehty, zobáky, zuby, rohy, parohy nebo schránky měkkýšů. (zdroj: wiki)
A: Jaká číslice je první za desetinnou čárkou?
B: Jaká číslice se objevuje nejvíckrát v prvních 10 číslech za desetinnou čárkou ?
C: Jaká číslice je před desetinnou čárkou?
D: Jaká číslice je na 314. pozici desetinného rozvoje zlatého řezu?
E: Kolik různých číslic je použito v základním vyjádření vzorce?

Boltzmannova konstanta
kB
Boltzmannova konstanta vyjadřuje vztah mezi teplotou a energií plynu. Vyjadřuje množství energie potřebné k zahřátí jedné částice ideálního plynu o jeden kelvin. Boltzmannova konstanta také úzce souvisí s entropií, protože stejně jako u entropie jde o množství energie na určitou teplotu. Byla pojmenována po rakouském fyzikovi Ludwigu Boltzmannovi, který se významně podílel na rozvoji statistické fyziky, kde tato konstanta hraje klíčovou roli.
kB
Její značka je k nebo kB. Vynásobením Boltzmannovy a Avogadrovy konstanty dostaneme univerzální plynovou konstantu, která udává totéž pro látkové množství jednoho molu. Díky tomu můžeme vyjádřit stavovou rovnici ideálního plynu. Boltzmannova konstanta také hraje svou roli ve statistické fyzice. Můžeme pomocí ní vyjadřovat entropii a také hraje roli ve fyzice polovodičů, protože se pomocí ní dá vyjádřit množství tepelné energie rozdělované mezi elektrony, která vytváří potenciál způsobující tzv. tepelné napětí. (zdroj: wiki)
A: Jaká číslice je první ve vyjádření Boltzmannovy konstanty v J/K?
B: Jaká číslice je poslední ve vyjádření Boltzmannovy konstanty v J/K (myšleno číslo před exponentem a jeho základem)?
C: Jaká číslice je druhá ve vyjádření Boltzmannovy konstanty v eV/K?
D: Jaká číslice je první ve vyjádření Boltzmannovy konstanty v Hz/K?


π (Pí)
π
O pí toho asi moc říkat nemusím, snad každý ho zná alespoň na dvě desetinná místa, pravidelně jsou i pořádány eventy 14. března na jeho počest.
Pí je matematická konstanta, která udává poměr obvodu jakéhokoli kruhu v eukleidovské rovině k jeho průměru; také je to hodnota poměru obsahu kruhu ke čtverci jeho poloměru. Její hodnota v desítkové soustavě je přibližně 3,14159265359. Mnoho matematických, vědeckých a inženýrských rovnic obsahuje pí, což z něj dělá jednu z nejdůležitějších matematických konstant. Je to iracionální číslo, což znamená, že ho nelze vyjádřit podílem dvou celých čísel.
π
To také znamená, že jej nelze vyjádřit konečným způsobem v desítkové soustavě, a to ani pomocí periody. Navíc je π dokonce transcendentní číslo, z čehož mimo jiné vyplývá, že ho nelze vyjádřit konečně dlouhou řadou algebraických operací s celými čísly. Konstantě se také někdy říká Ludolfovo číslo, spíše historické (ale např. v angličtině používané) je označení Archimédova konstanta. Malým řeckým písmenem se zapisuje od roku 1707 podle řeckého slova περίμετρος (perimetros).
A: Jaká číslice se jako první v pí opakuje 9x za sebou?
B: Jaká číslice je těsně před touto sérií 9 čísel?
C: Jaká číslice je těsně za touto sérií 9 čísel?
D: V první tisícovce se pouze jedna číslice opakuje 6x za sebou, která?


Rychlost světla
C0
Rychlost světla (nebo jiného elektromagnetického záření) ve vakuu je definována jako fázová rychlost postupného elektromagnetického vlnění ve vakuu. Označuje se písmenem c0, pro stručnost se často píše jen c (značka je pravděpodobně z latinského celeritas, což znamená rychlost, nebo z constans, znamenající konstanta).
Tato rychlost dává přirozený poměr měřítek prostoru a času a je nejvyšší možnou rychlostí šíření signálu či informace.
Rychlostí světla se šíří také gravitace v obecné teorii relativity. Zákony elektromagnetismu uvádějí, že rychlost elektromagnetického záření c0 nezávisí na rychlosti objektu vyzařujícího záření. Proto například světlo vyzařující z rychle se pohybujícího zdroje se šíří stejnou rychlosti jako světlo vyzařované ze statického zdroje, i když podle relativistického Dopplerova jevu se barva, frekvence, energie a hybnost světla změní.
c0
Jestliže se zkombinuje pozorování s principem relativity, všichni pozorovatelé naměří shodnou rychlost světla ve vakuu, nezávisle na vztažné soustavě pozorovatele nebo rychlosti objektu vyzařujícího světlo. Proto se na c0 může nahlížet jako na fyzikální konstantu a tento fakt je základem speciální teorie relativity.
Astronomické jednotky jsou někdy udávány ve světelných letech. Světelný rok je vzdálenost, kterou urazí světlo za jeden rok, t. j. přibližně 9,46 × 1012 kilometru.
Konečná rychlost světla je důležitá v komunikaci. Například světlo by oběhlo Zeměkouli kolem rovníku za sekundu asi 7,5krát. Skutečný čas přenosu ale trvá déle. Částečně je to způsobeno tím, že se světlo v optickém vlákně šíří asi o 30 % pomaleji a přímá spojení nejsou v globální komunikaci častá, ale i kvůli zdržením v síťových přepínačích a směrovačích. Typický čas odezvy počítače mezi Austrálií a USA byl v roce 2004 asi 0,18 sekundy. Rychlost informace navíc ovlivňuje řešení částí systému, kde dochází k bezdrátové komunikaci.
Konečná rychlost světla byla zřetelná například při komunikaci mezi pozemním centrem Houston a Neilem Armstrongem, když se stal prvním člověkem na Měsíci. Na každou odpověď museli v Houstonu čekat téměř 3 sekundy, i když astronauti odpovídali okamžitě. (zdroj: wiki)
A: Ciferace rychlosti světla ve vakuu v m/s.
B: Ciferace rychlosti světla ve vakuu v km/h.
C: Za jak dlouho uletí světlo vzdálenost ze Slunce k Zemi (zaokrouhleno na celé minuty)?
V jakých jednotkách se udává světelný rok?
dny D=4
kilogramy D=5
metry za sekundu D=6
metry D=7


Hmotnost elektronu, protonu a neutronu
Elektron je subatomární částice se záporným elektrickým nábojem. Elektrony tvoří obal atomu kolem atomového jádra. Elektrony jsou nositeli náboje při vedení elektrického proudu v kovech, polovodičích a v elektrických výbojích v plynech i ve vakuu (např. katodové záření). Také radioaktivní záření beta (β–) je tvořeno elektrony. Elektron jakožto elementární částice patří mezi leptony, tj. mezi částice, které nejsou schopny silné interakce, ale pouze elektromagnetické a slabé interakce. Slovo elektron pochází z řeckého slova „jantar“ (ήλεκτρον), který zavedl William Gilbert. Elektrické jevy poprvé popsal Thales Milétský na vlastnostech jantarového nástroje, užívaného při předení lnu.
Proton
Ve fyzice je proton subatomární částice s kladným elementárním elektrickým nábojem. Proton je podle současných poznatků částicí stabilní. Podle některých teorií se však může rozpadat s poločasem rozpadu přes 1031 roků. Rozpad protonu nebyl dosud pozorován, stále se prodlužující experimentálně zjištěná minimální hodnota střední doby života protonu (τ > 1031 roků obecně, pro jednotlivé modely a kanály rozpadu až 1034) již vyloučila mnohé z nejjednodušších variant teorie velkého sjednocení, zejména pokud se jedná o varianty bez předpokladu supersymetrie. Horní hranice střední doby života, pokud je proton skutečně nestabilní, může být podle teorií až 1039 roků. Proton řadíme mezi baryony, konkrétně baryony N v základním stavu, tedy do nukleonů (spolu s neutronem).
Neutron
Neutron je subatomární částice bez elektrického náboje (neutrální částice), jedna ze základních stavebních částic atomového jádra (nukleon) a tím téměř veškeré známé hmoty. Atomy lišící se jen počtem neutronů se nazývají izotopy. Neutrony se z atomu uvolňují při jaderných reakcích, volné neutrony způsobují řetězení štěpné reakce a jejich samostatný proud se nazývá neutronové záření.
Mimo atomové jádro je neutron nestabilní se střední dobou života 881,5 ± 1,5 sekundy (zhruba 14,7 minuty), přičemž se rozpadá na proton, elektron a elektronové antineutrino. Neutron se řadí mezi baryony – interaguje silnou interakcí. Protony a neutrony se označují společným názvem nukleony. (zdroj: wiki)
ABCD: Kolikrát je proton těžší než elektron?
E: Poslední číslice v hmotnosti neutronu v jednotkách MeV/c2, pokud zaokrouhlíme na celé číslo.
Eulerovo číslo
e
Eulerovo číslo je jedna ze základních matematických konstant. Je to základ přirozeného logaritmu a objevuje se nejčastěji při výpočtech limit, derivací a integrálů.
Jedna z definic říká, že je to jediné reálné číslo takové, že funkce a^x má hodnotu směrnice tečny v bodě nula rovnu jedné.
A: Kolik je přirozený logaritmus Eulerova čísla?
B: Jaká číslice se objevuje nejvíc krát v prvních 10 číslech za desetinnou čárkou?
C: Jaká číslice se jako první opakuje 2x za sebou?
D: Jaká číslice je na 314. pozici desetinného rozvoje Eulerova čísla?
E: Jaká číslice je před desetinnou čárkou?
Avogadrova konstanta
NA
Avogadrova konstanta vyjadřuje počet částic v jednotkovém látkovém množství (v 1 molu). Je pojmenována po italském fyzikovi Avogadrovi, její hodnotu však poprvé zjistil Johann Josef Loschmidt roku 1865.
Avogadrova konstanta je definována jako celkový počet atomů v dvanácti gramech nuklidu uhlíku, tedy stabilního izotopu, který obsahuje v jádře šest protonů a šest neutronů.
Avogadrova konstanta se značí NA (případně L) a v soustavě SI se udává v jednotkách mol−1.
NA
Avogadrova konstanta je měřítkem používaným při makroskopickém a mikroskopickém pozorování přírody. Jako taková poskytuje nástroj pro vytváření vztahů mezi ostatními fyzikálními veličinami a konstantami. (zdroj: wiki)
AB: Jaké číslo je využito jako exponent v základním vyjádření Avogadrovy konstanty?
CD: Kolik nul je za poslední nenulovou číslicí (a před desetinnou čárkou), pokud bychom použili vyjádření neobsahující zmíněné 10^AB?
E: Jaká číslice je na 314. pozici desetinného rozvoje Avogadrovy konstanty?
F: Rozdíl v počtu protonů a neutronů v nuklidu uhlíku, dříve používaného pro vyjádření konstanty?
G: Jaká čísice je před desetinnou čárkou v základním vyjádření Avogadrovy konstanty?
Elementární náboj
e
Elementární náboj je nejmenší možný elektrický náboj jedné volné částice. Elementární (elektrický) náboj je roven velikosti elektrického náboje elektronu. Elektron má záporný elementární náboj, proton má kladný elementární náboj. Značka veličiny je e (pro elektron -e, pro proton +e).
Elektrický náboj každého tělesa je celočíselným násobkem elementárního náboje. U běžných zelektrovaných těles se toto kvantování elektrického náboje neprojeví kvůli velkému množství částic a tedy značné „jemnosti“ celkového náboje. To nás opravňuje přiřazovat celkovému náboji makroskopického tělesa hodnoty, které nemusejí být celočíselnými násobky elementárního náboje. (zdroj: wiki)
A: Jaká číslice je v základním vyjádření první za desetinnou čárkou?
B: Počet cifer za desetinnou čárkou v základním vyjádření konstanty?
C: Jaká číslice je v základním vyjádření třetí za desetinnou čárkou?
D: Jaká číslice je v základním vyjádření před desetinnou čárkou?
Planckova konstanta
h
Planckova konstanta je jedna ze základních fyzikálních konstant. Jako fyzikální veličina má rozměr momentu hybnosti nebo akce. Planckova konstanta byla poprvé zavedena Maxem Planckem jako konstanta vyzařovacího zákona černého tělesa.
Nejpřesnější způsob měření Planckovy konstanty na počátku 21. století představovaly wattové váhy, které porovnávají tíži tělesa s magnetickou silou. K měření elektrických veličin se přitom využívá Josephsonův jev a kvantový Hallův jev, což umožňuje dát hmotnost do přímého vztahu s Planckovou konstantou. Když Mezinárodní úřad pro míry a váhy uvažoval o e kilogramu, jednou z možností bylo právě stanovení přesné hodnoty Planckovy konstanty. K zavedení této definice došlo v roce 2019. Její hodnotu by pak již není třeba měřit a wattové váhy slouží pro přesnou realizaci prototypu kilogramu.
Planckova konstanta se hojně vyskytuje v kvantové mechanice, a to v Schrödingerově rovnici, při přepočtu vlnové délky fotonu na jeho energii s využitím rychlosti světla, hybnosti na vlnový vektor apod. (zdroj: wiki)
A: V jakém roce došlo ke zpřesnění hodnoty konstanty? 201A
B: Jaká číslice je před desetinnou čárkou ve vyjádření konstanty v elektronvoltech na hertz?
C: Jaký je vztah mezi Planckovou a redukovanou Planckovou konstantou? Cπ
D: Jaká číslice je před desetinnou čárkou ve vyjádření konstanty v joulech za sekundu?
E: Jaká nejnižší číslice se vyskytuje v obou vyjádřeních konstanty? (Exponenciální část nebereme v úvahu)
Rydbergova konstanta
R∞
Rydbergova konstanta je fyzikální konstanta pojmenovaná po švédském fyzikovi Johannesu Rydbergovi. Představuje nejvyšší možný vlnočet (převrácená hodnota vlnové délky) elektromagnetického záření, které může vyzářit nejjednodušší atom – atom vodíku. Rydbergova konstanta a další příbuzné konstanty, jako jsou Rydbergova frekvence, Rydbergova energie a Hartreeova energie, mají zásadní význam ve spektroskopii. (zdroj: wiki)
A: Jaká číslice je první za desetinnou čárkou?
B: Jaká je nejvyšší číslice před desetinnou čárkou?
C: Jaká je nejnižší číslice před desetinnou čárkou?
D: Kolik je číslic před desetinnou čárkou?
E: Jaká je první číslice Rydbergovy frekvence?
Energie elektronu, protonu a neutronu
Elektron je subatomární částice se záporným elektrickým nábojem. Elektrony tvoří obal atomu kolem atomového jádra. Elektrony jsou nositeli náboje při vedení elektrického proudu v kovech, polovodičích a v elektrických výbojích v plynech i ve vakuu (např. katodové záření). Také radioaktivní záření beta (β–) je tvořeno elektrony. Elektron jakožto elementární částice patří mezi leptony, tj. mezi částice, které nejsou schopny silné interakce, ale pouze elektromagnetické a slabé interakce. Slovo elektron pochází z řeckého slova „jantar“ (ήλεκτρον), který zavedl William Gilbert. Elektrické jevy poprvé popsal Thales Milétský na vlastnostech jantarového nástroje, užívaného při předení lnu.
Proton
Ve fyzice je proton subatomární částice s kladným elementárním elektrickým nábojem. Proton je podle současných poznatků částicí stabilní. Podle některých teorií se však může rozpadat s poločasem rozpadu přes 1031 roků. Rozpad protonu nebyl dosud pozorován, stále se prodlužující experimentálně zjištěná minimální hodnota střední doby života protonu (τ > 1031 roků obecně, pro jednotlivé modely a kanály rozpadu až 1034) již vyloučila mnohé z nejjednodušších variant teorie velkého sjednocení, zejména pokud se jedná o varianty bez předpokladu supersymetrie. Horní hranice střední doby života, pokud je proton skutečně nestabilní, může být podle teorií až 1039 roků. Proton řadíme mezi a baryony, konkrétně baryony N v základním stavu, tedy do nukleonů (spolu s neutronem).
Neutron
Neutron je subatomární částice bez elektrického náboje (neutrální částice), jedna ze základních stavebních částic atomového jádra (nukleon) a tím téměř veškeré známé hmoty. Atomy lišící se jen počtem neutronů se nazývají izotopy. Neutrony se z atomu uvolňují při jaderných reakcích, volné neutrony způsobují řetězení štěpné reakce a jejich samostatný proud se nazývá neutronové záření.
Mimo atomové jádro je neutron nestabilní se střední dobou života 881,5 ± 1,5 sekundy (zhruba 14,7 minuty), přičemž se rozpadá na proton, elektron a elektronové antineutrino. Neutron se řadí mezi baryony – interaguje silnou interakcí. Protony a neutrony se označují společným názvem nukleony. (zdroj: wiki)
A: Která částice má největší klidovou energii?
Elektron A=8
Proton A=4
Neutron A=0
B: Jaká je první nenulová číslice v hodnotě klidové energie elektronu udané v joulech?
C: Jaká je první nenulová číslice v hodnotě klidové energie protonu udané v joulech?
D: Rozdíl v klidové energii protonu a neutronu je malý. Najdi u hodnot udávaných v joulech první číslici, která se liší, a zapiš si rozdíl mezi nimi.
Gravitační konstanta
G
Gravitační konstanta (též Newtonova gravitační konstanta) je v Newtonově gravitačním zákoně konstanta úměrnosti mezi gravitační silou a součinem hmotností interagujících těles děleným kvadrátem jejich vzdálenosti. Je to jedna ze tří základních fyzikálních konstant, které určují volbu našich jednotek vůči jednotkám Planckovým.
První praktické měření gravitační konstanty provedl Henry Cavendish. Jeho aparatura se skládala ze dvou olověných kuliček o hmotnosti 730 g, umístěných na vodorovném rameni, zavěšeném na tenkém vlákně. Na rameni, které s vláknem fungovalo jako torzní váhy, bylo umístěno zrcátko. Paprsek světla, odražený od zrcátka, indikoval výchylku, která byla měřena pomocí dalekohledu. Ke kuličkám byla střídavě z jedné a druhé strany přibližována dvojice větších olověných koulí o hmotnostech 158 kg, umístěná na nezávislém otočném rameni.
1896
V roce 1896 použili Richarz a Krigar-Menzel dvojici kilogramových závaží, zavěšených na různě dlouhých vláknech na rovnoramenných vahách. K tělesům byl umístěn velký olověný blok tak, aby jedno těleso bylo nad a druhé pod ním.
Jednodušší metodu měření navrhl fyzik P. Jolly. Na velmi citlivých rovnoramenných vahách vyvážil kouli o hmotnosti m. Pod ni pak umístil masivní kouli o hmotnosti M, jejíž střed byl ve vzdálenosti r od menší koule. Působením gravitační síly mezi oběma koulemi se ručička vah vychýlí. Rovnováha je pak obnovena přidáním závaží o hmotnosti Z na misku vah. Mezi oběma koulemi působí gravitační síla. Mezi Zemí a závažím Z pak tíhová síla. Jolly použil koule o hmotnostech M = 6 tun, m = 10 kg, jejich vzdálenost r = 60 cm a závaží Z = 1,1 mg. Po dosazení mu tedy vyšla relativně přesná hodnota G. (zdroj: wiki)
ABCD: V jakém roce proběhlo první praktické měření konstanty?
E: Ciferace hodnoty gravitační konstanty.
F: Nejnižší nenulová cifra gravitační konstanty.
Jen upozorňuji, že se u E a F nepočítá s exponenciální částí čísla.
Hostouňský výlet se nám líbil.
P.S. Matematicko-fyzikálně-chemické problematiky se neboj… od čeho je Wikipedie, že? 🙂
Nalezené kešky
- GC33WQ5 Hostounske jasany Hostouň
- GC1K7ZZ Schindleruv seznam Hostouň
- GC782B1 Pi #16 Bonus – Erdősovo číslo Hostouň
- GC5T6BF Rizeni letoveho provozu II. Hostouň
- GC7824T Pi #08 Faradayova konstanta Hostouň
- GC78273 Pi #13 Permeabilita vakua Hostouň
- GC7827F Pi #14 Permitivita vakua Hostouň
- GC78232 Pi #03 Zlatý řez Hostouň
- GC78245 Pi #06 Boltzmannova konstanta
- GC7821R Pi #01 aneb 3,141592…
- GC7823B Pi #04 Rychlost světla
- GC25N3V Male Pritocno – DC-3 Accident Hostouň
- GC39D3H 101 – 074 Sparky Hostouň
- GC7826A Pi #11 Hmotnost elektronu, protonu a neutronu
- GC7822B Pi #02 Eulerovo číslo
- GC7823V Pi #05 Avogadrova konstanta
- GC7825W Pi #10 Elementární náboj
- GC7824M Pi #07 Planckova konstanta
- GC7825H Pi #09 Rydbergova konstanta
- GC7826Y Pi #12 Energie elektronu, protonu a neutronu
- GC7827Q Pi #15 Gravitační konstanta
- GC5JWMQ Svatebni den czjawa & Brouci Hostouň















